Многоцелевые задачи ЛП - Математические методы

Решение многоцелевых задач линейного программирования с помощью метода последовательных уступок.

Условия задачи:

- Система ограничений, вида:

A*x + B*y + C [

- Набор критериев оптимальности в порядке уменьшения важности, вида:

A*x + B*y + C --> [Max, Min]

- Набор процентов уступок (для каждого критерия)

- Найти точку (x, y), в которой достигается оптимальное значение

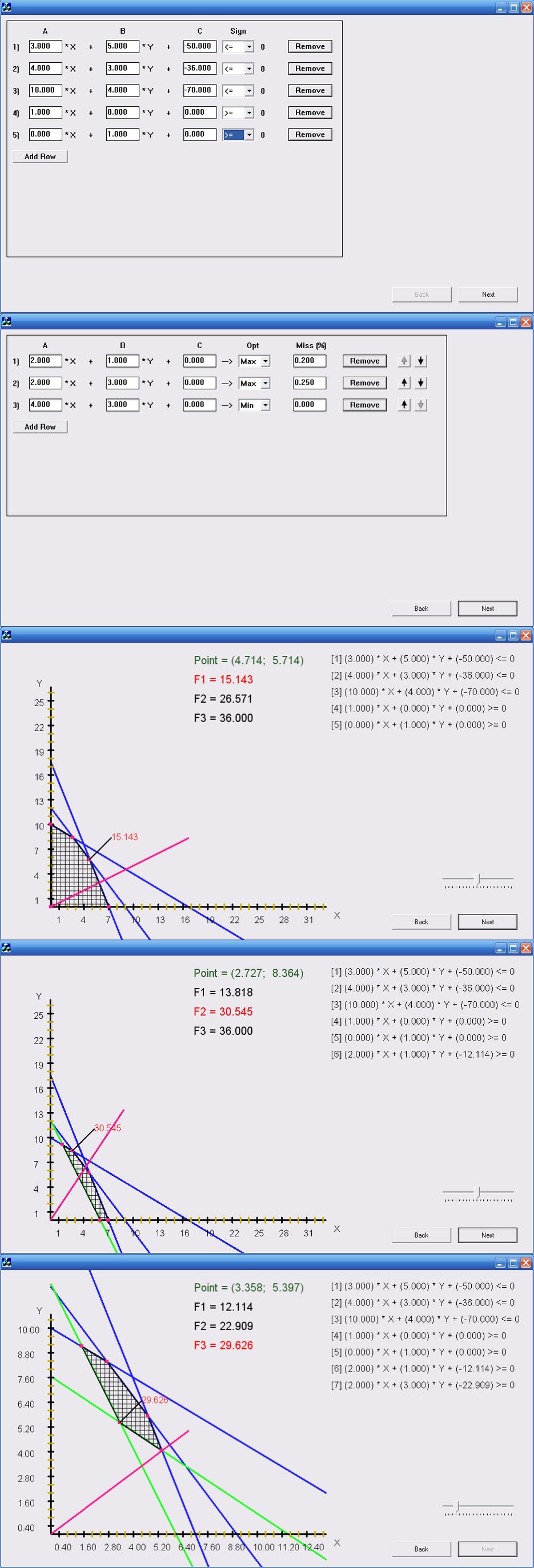
Графически представляется как многоугольник, ограниченный линиями по условиям задачи.

Каждый шаг решения ведется графическим методом решения задач линейного программирования (в программе реализация - отыскание оптимума в граничных точках многоугольника).

После каждого шага в зависимости от полученного оптимума текущего критерия и его процента уступки вводится новое ограничение в систему и получается новый многоугольник решений.

Реализация - MFC.

***

Возможно вводить до 10 изначальных условий в системе ограничений.

Возможно вводить до 5 критериев оптимальности.

Возможность масштабирования графика.